Melvyn Bragg's superb programme, "In Our Time" did an episode on imaginary numbers this week. Interesting as it was, I don't think the utility of imaginary numbers really came across. As this blog occasionally deals with other imaginary items, I don't feel it's too off topic to try and provide a short explanation of imaginary numbers for the non-mathematically inclined out there.
"Imaginary" numbers are numbers that are multiples of the square root of -1, usually denoted by the letter i. For centuries, it was known that many solutions of equations, such as x squared = -1, required i. These were simply discarded as it was assumed they had no real meaning. There seemed to be no number that, when squared, could possibly equal -1.
Mathematicians simply invented the number i and started to play with it just as if it were one of the "real" numbers. When we add real and imaginary numbers together (e.g. 2 + 3i ) we get the so called "complex" numbers. Carl Friedrich Gauss was able to show (in his doctoral thesis no less) that all equations involving powers of x had solutions in the complex numbers. The algebra of complex numbers can, in this sense, be thought of as complete. This theorem goes by the rather grand title, "The Fundamental Theorem of Algebra".
The real usefulness of complex numbers only become apparent once we adopt a visual representation for them. Real numbers can be thought of as being placed on a line that goes from left to right,

stretching off to infinity in both directions. All fractions, irrational numbers (such as square root of 2) and transcendental numbers (such as pi) have their appropriate place on the line, but there is no number on the line that squares to -1. Several mathematicians had the idea of drawing another line at ninety degrees to the real numbers and placing the imaginary numbers there. This is called the Argand plane.
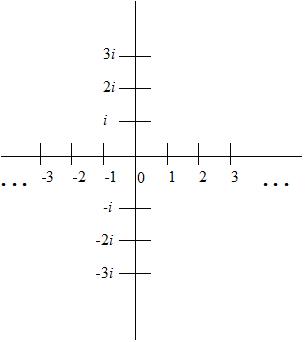
To add or subtract complex numbers you just add or subtract their corresponding real and imaginary parts. Multiplication is a bit more interesting. Here are two complex numbers:
1 + i and -1 + i
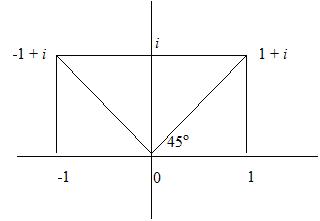
The absolute "length" of these numbers as plotted on the Argand plane is just found using Pythagoras' theorem:
square root (1 squared + 1 squared) = root 2.
They make angles of 45 degrees and 135 degrees with the positive real axis.
To multiply them we just use the normal distributive rule of ordinary arithmetic.
(1 + i) x (-1 + i)
= 1 x (-1 + i) + i x (-1 + i)
= -1 + i - i - 1 (remembering that i x i = -1)
= -2
This is a number that has a length which is the product of the two original numbers (root 2 times root 2 = 2) and the sum of their angles (45 degrees + 135 degrees = 180 degrees).
Although we've only shown it for a special case, a little bit of trigonometry shows it to be true in general. To multiply two complex numbers, you multiply their lengths and add their angles. But now consider complex numbers that all lie on a circle of radius one.
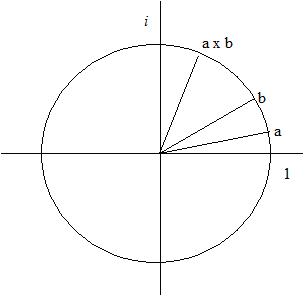
All these complex numbers have length one. Multiply any two of them together and you get another complex number with length one but with the two angles added together. Those of you who remember your logarithms and exponentials might see a connection here.
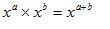
To multiply two exponentials of the same number, you just add their exponents. We have something very similar here with two unit length complex numbers: you just do an addition, but this time it's of their angles.
If you remember your basic trigonometry, you'll see that the complex numbers on the unit circle have real and imaginary parts corresponding to the sine and cosine of their angles.
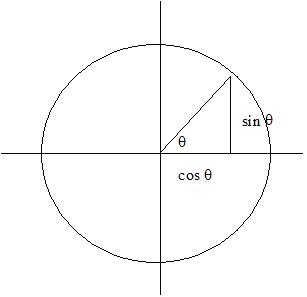
So we can express any complex number of unit length in terms of a single parameter, namely its angle.
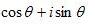
And we can multiply two of them simply by adding their angles. This connection between exponentiation and trigonometry gives us the incredibly useful formula (Euler's formula):
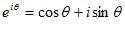
(e is the base of the natural logarithms).
Why is this so incredibly useful? The reason is that it is much much easier to manipulate exponentials than to manipulate trigonometric functions. Nature is full of periodic, wavelike phenomena. These can be broken down into sums of sines and cosines.
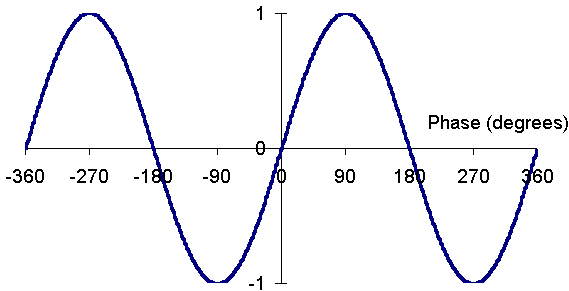
Expressing them as complex exponentials makes possible much of the world of electrical and electronic engineering, heat flow, fluid flow, quantum mechanics. Almost anything that is periodic or wavelike would be incredibly hard to work with without Euler's famous formula.
It might be going too far to say that modern technology, science and engineering would be impossible without imaginary numbers, but it would certainly make life a lot harder.
"Imaginary" numbers are numbers that are multiples of the square root of -1, usually denoted by the letter i. For centuries, it was known that many solutions of equations, such as x squared = -1, required i. These were simply discarded as it was assumed they had no real meaning. There seemed to be no number that, when squared, could possibly equal -1.
Mathematicians simply invented the number i and started to play with it just as if it were one of the "real" numbers. When we add real and imaginary numbers together (e.g. 2 + 3i ) we get the so called "complex" numbers. Carl Friedrich Gauss was able to show (in his doctoral thesis no less) that all equations involving powers of x had solutions in the complex numbers. The algebra of complex numbers can, in this sense, be thought of as complete. This theorem goes by the rather grand title, "The Fundamental Theorem of Algebra".
The real usefulness of complex numbers only become apparent once we adopt a visual representation for them. Real numbers can be thought of as being placed on a line that goes from left to right,

stretching off to infinity in both directions. All fractions, irrational numbers (such as square root of 2) and transcendental numbers (such as pi) have their appropriate place on the line, but there is no number on the line that squares to -1. Several mathematicians had the idea of drawing another line at ninety degrees to the real numbers and placing the imaginary numbers there. This is called the Argand plane.
To add or subtract complex numbers you just add or subtract their corresponding real and imaginary parts. Multiplication is a bit more interesting. Here are two complex numbers:
1 + i and -1 + i

The absolute "length" of these numbers as plotted on the Argand plane is just found using Pythagoras' theorem:
square root (1 squared + 1 squared) = root 2.
They make angles of 45 degrees and 135 degrees with the positive real axis.
To multiply them we just use the normal distributive rule of ordinary arithmetic.
(1 + i) x (-1 + i)
= 1 x (-1 + i) + i x (-1 + i)
= -1 + i - i - 1 (remembering that i x i = -1)
= -2
This is a number that has a length which is the product of the two original numbers (root 2 times root 2 = 2) and the sum of their angles (45 degrees + 135 degrees = 180 degrees).
Although we've only shown it for a special case, a little bit of trigonometry shows it to be true in general. To multiply two complex numbers, you multiply their lengths and add their angles. But now consider complex numbers that all lie on a circle of radius one.

All these complex numbers have length one. Multiply any two of them together and you get another complex number with length one but with the two angles added together. Those of you who remember your logarithms and exponentials might see a connection here.
To multiply two exponentials of the same number, you just add their exponents. We have something very similar here with two unit length complex numbers: you just do an addition, but this time it's of their angles.
If you remember your basic trigonometry, you'll see that the complex numbers on the unit circle have real and imaginary parts corresponding to the sine and cosine of their angles.

So we can express any complex number of unit length in terms of a single parameter, namely its angle.
And we can multiply two of them simply by adding their angles. This connection between exponentiation and trigonometry gives us the incredibly useful formula (Euler's formula):
(e is the base of the natural logarithms).
Why is this so incredibly useful? The reason is that it is much much easier to manipulate exponentials than to manipulate trigonometric functions. Nature is full of periodic, wavelike phenomena. These can be broken down into sums of sines and cosines.

Expressing them as complex exponentials makes possible much of the world of electrical and electronic engineering, heat flow, fluid flow, quantum mechanics. Almost anything that is periodic or wavelike would be incredibly hard to work with without Euler's famous formula.
It might be going too far to say that modern technology, science and engineering would be impossible without imaginary numbers, but it would certainly make life a lot harder.






