Twin A sees B's clock as running slower. The number we have to use to find values on B's clock is 5/3 in this case. We can take any time on A's clock, divide by 5/3, and we get the time that A sees on B's clock. So when B arrives at the star, A thinks the time on B's clock is 5/4 divided by 5/3, which is 3/4.
A's clock therefore shows 10/4, or 2 1/2 years for the round trip, but sees B's clock as showing 6/4, or 1 1/2 years for the round trip. B will be younger than A by one year.
In the diagram below (and all future diagrams):
Arrows in red show changes in twin A. Coordinates in red show coordinates as seen by A.
Arrows in blue show changes in twin B. Coordinates in blue show coordinates as seen by B. (Just remember "B" for Blue.)
The first set of coordinates will normally be those of the stationary observer in that frame of reference.
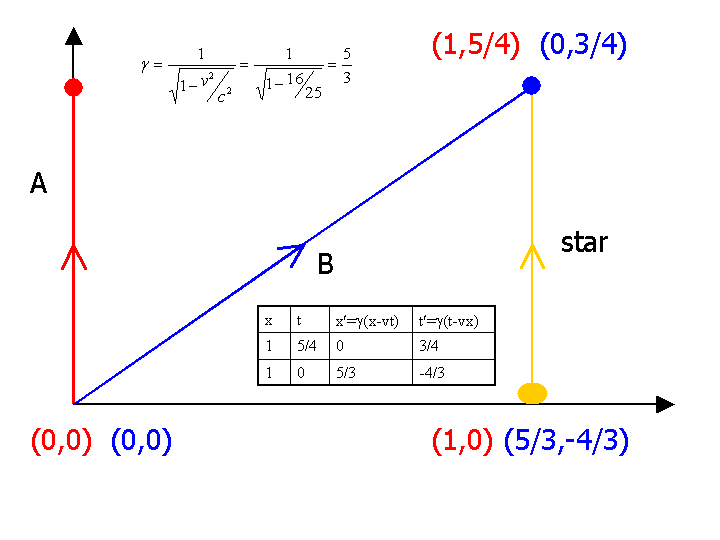
As well as the beginning and end of B's journey, there is a third event on the above diagram: the starting point of the distant star. Twin A sees the star as being one light year away at time zero (and at all other times). Einstein gave us the formulas for converting space and time coordinates from a stationary observer to a moving one. Using these formulas, the starting point of the star has some very peculiar co-ordinates from B's point of view. It starts off farther away and over a year in the past!
The diagram really expresses the different spacetime coordinates for A and B as if B had always been moving at 4/5 the speed of light. Although this might seem odd if you're unfamiliar with relativity, the idea of the same thing happening at different times for different observers, really is one of the consequences of the theory.
The important thing from the point of view of the twins paradox, is that twin B wasn't moving at 4/5 light speed just over a year ago. This means that something very strange must happen as twin B starts to accelerate.
start
prev
next
A's clock therefore shows 10/4, or 2 1/2 years for the round trip, but sees B's clock as showing 6/4, or 1 1/2 years for the round trip. B will be younger than A by one year.
In the diagram below (and all future diagrams):
Arrows in red show changes in twin A. Coordinates in red show coordinates as seen by A.
Arrows in blue show changes in twin B. Coordinates in blue show coordinates as seen by B. (Just remember "B" for Blue.)
The first set of coordinates will normally be those of the stationary observer in that frame of reference.
As well as the beginning and end of B's journey, there is a third event on the above diagram: the starting point of the distant star. Twin A sees the star as being one light year away at time zero (and at all other times). Einstein gave us the formulas for converting space and time coordinates from a stationary observer to a moving one. Using these formulas, the starting point of the star has some very peculiar co-ordinates from B's point of view. It starts off farther away and over a year in the past!
The diagram really expresses the different spacetime coordinates for A and B as if B had always been moving at 4/5 the speed of light. Although this might seem odd if you're unfamiliar with relativity, the idea of the same thing happening at different times for different observers, really is one of the consequences of the theory.
The important thing from the point of view of the twins paradox, is that twin B wasn't moving at 4/5 light speed just over a year ago. This means that something very strange must happen as twin B starts to accelerate.
start
prev
next






